Distribution Plots
Let’s discuss some plots that allow us to visualize the distribution of a data set. These plots are:
- distplot
- jointplot
- pairplot
- rugplot
- kdeplot
Imports
import seaborn as sns
%matplotlib inline
Data
Seaborn comes with built-in data sets!
tips = sns.load_dataset('tips')
tips.head()
| total_bill | tip | sex | smoker | day | time | size | |
|---|---|---|---|---|---|---|---|
| 0 | 16.99 | 1.01 | Female | No | Sun | Dinner | 2 |
| 1 | 10.34 | 1.66 | Male | No | Sun | Dinner | 3 |
| 2 | 21.01 | 3.50 | Male | No | Sun | Dinner | 3 |
| 3 | 23.68 | 3.31 | Male | No | Sun | Dinner | 2 |
| 4 | 24.59 | 3.61 | Female | No | Sun | Dinner | 4 |
distplot
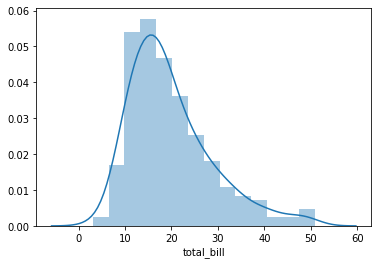
The distplot shows the distribution of a univariate set of observations.
sns.distplot(tips['total_bill'])
# Safe to ignore warnings
<matplotlib.axes._subplots.AxesSubplot at 0x7f094c6b3a90>
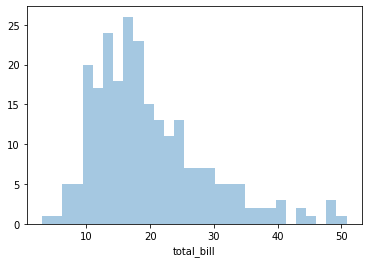
To remove the kde layer and just have the histogram use:
sns.distplot(tips['total_bill'],kde=False,bins=30)
<matplotlib.axes._subplots.AxesSubplot at 0x7f094a543e10>
jointplot
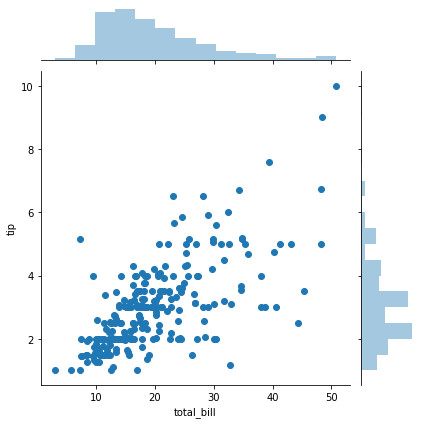
jointplot() allows you to basically match up two distplots for bivariate data. With your choice of what kind parameter to compare with:
- “scatter”
- “reg”
- “resid”
- “kde”
- “hex”
sns.jointplot(x='total_bill',y='tip',data=tips,kind='scatter')
<seaborn.axisgrid.JointGrid at 0x7f0949ed63c8>
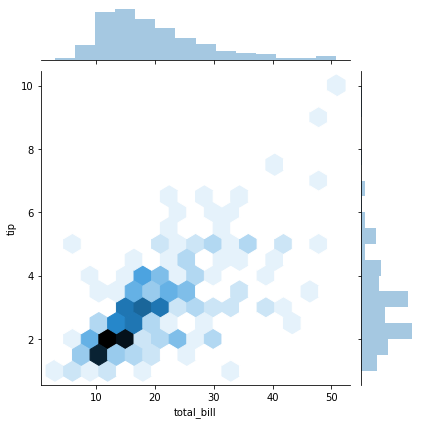
sns.jointplot(x='total_bill',y='tip',data=tips,kind='hex')
<seaborn.axisgrid.JointGrid at 0x7f094cf28cc0>
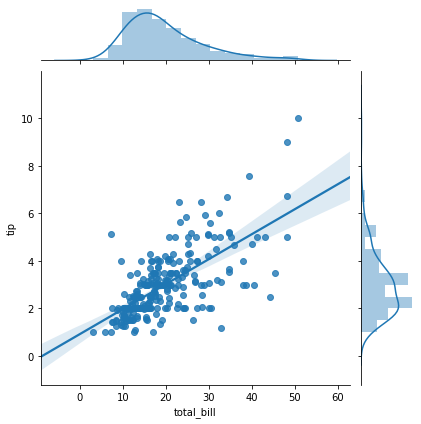
sns.jointplot(x='total_bill',y='tip',data=tips,kind='reg')
<seaborn.axisgrid.JointGrid at 0x7f0949ce0eb8>
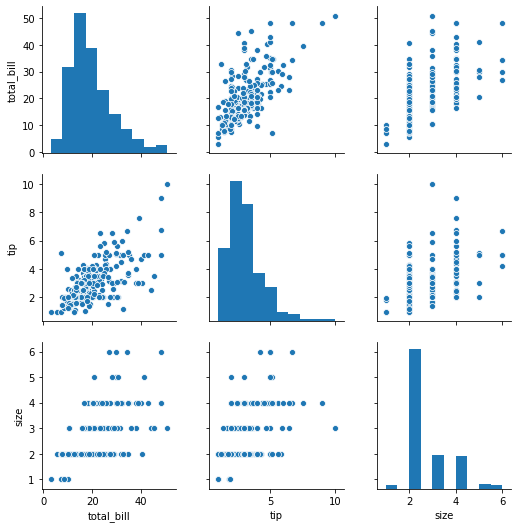
pairplot
pairplot will plot pairwise relationships across an entire dataframe (for the numerical columns) and supports a color hue argument (for categorical columns).
sns.pairplot(tips)
<seaborn.axisgrid.PairGrid at 0x7f0949a907f0>
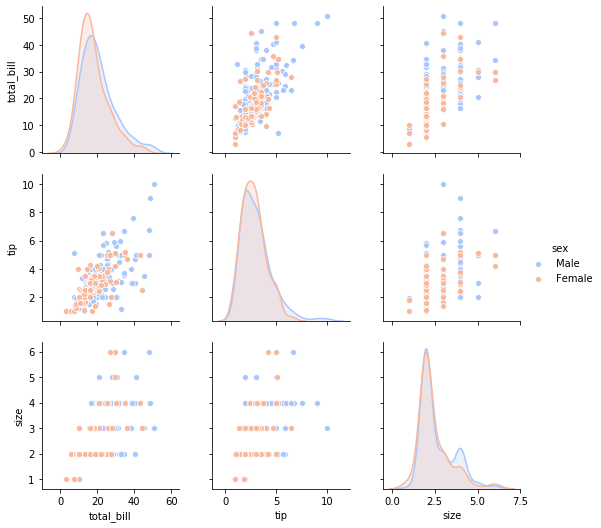
sns.pairplot(tips,hue='sex',palette='coolwarm')
<seaborn.axisgrid.PairGrid at 0x7f094968dda0>
rugplot
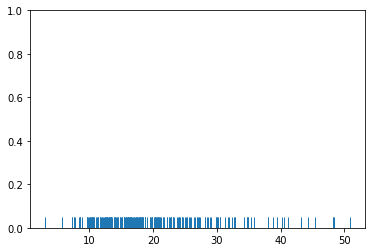
rugplots are actually a very simple concept, they just draw a dash mark for every point on a univariate distribution. They are the building block of a KDE plot:
sns.rugplot(tips['total_bill'])
<matplotlib.axes._subplots.AxesSubplot at 0x7f094913c898>
kdeplot
kdeplots are Kernel Density Estimation plots. These KDE plots replace every single observation with a Gaussian (Normal) distribution centered around that value. For example:
# Don't worry about understanding this code!
# It's just for the diagram below
import numpy as np
import matplotlib.pyplot as plt
from scipy import stats
#Create dataset
dataset = np.random.randn(25)
# Create another rugplot
sns.rugplot(dataset);
# Set up the x-axis for the plot
x_min = dataset.min() - 2
x_max = dataset.max() + 2
# 100 equally spaced points from x_min to x_max
x_axis = np.linspace(x_min,x_max,100)
# Set up the bandwidth, for info on this:
url = 'http://en.wikipedia.org/wiki/Kernel_density_estimation#Practical_estimation_of_the_bandwidth'
bandwidth = ((4*dataset.std()**5)/(3*len(dataset)))**.2
# Create an empty kernel list
kernel_list = []
# Plot each basis function
for data_point in dataset:
# Create a kernel for each point and append to list
kernel = stats.norm(data_point,bandwidth).pdf(x_axis)
kernel_list.append(kernel)
#Scale for plotting
kernel = kernel / kernel.max()
kernel = kernel * .4
plt.plot(x_axis,kernel,color = 'grey',alpha=0.5)
plt.ylim(0,1)
(0, 1)
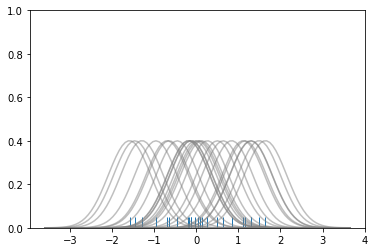
# To get the kde plot we can sum these basis functions.
# Plot the sum of the basis function
sum_of_kde = np.sum(kernel_list,axis=0)
# Plot figure
fig = plt.plot(x_axis,sum_of_kde,color='indianred')
# Add the initial rugplot
sns.rugplot(dataset,c = 'indianred')
# Get rid of y-tick marks
plt.yticks([])
# Set title
plt.suptitle("Sum of the Basis Functions")
Text(0.5, 0.98, 'Sum of the Basis Functions')
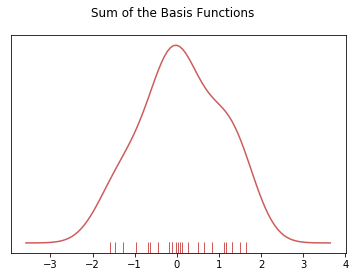
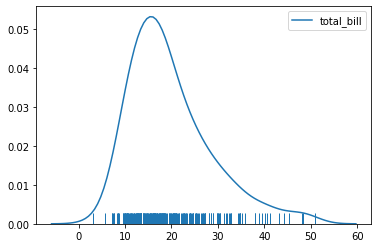
So with our tips dataset:
sns.kdeplot(tips['total_bill'])
sns.rugplot(tips['total_bill'])
<matplotlib.axes._subplots.AxesSubplot at 0x7f09491856a0>
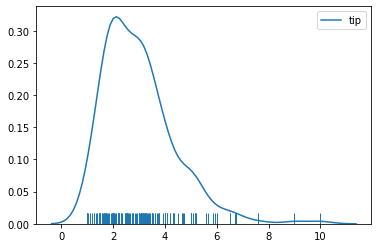
sns.kdeplot(tips['tip'])
sns.rugplot(tips['tip'])
<matplotlib.axes._subplots.AxesSubplot at 0x7f0948023e80>